Center Of Mass For Triangle

Now, let's get some do on computing centre of mass of objects.

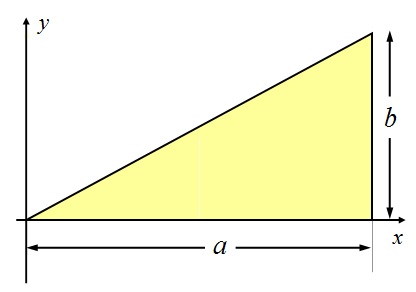
Right angle triangle

An object of mass $M$ is in the shape of a right-angle triangle whose dimensions are shown in the figure. Locate the coordinates of the centre of mass, assuming that the object has a uniform mass per unit of measurement expanse.

Recall that the equations for centre of mass:

$$\begin{aligned} x_{CM} &= \frac{1}{M} \int ten \, dm \\ y_{CM} &= \frac{1}{G} \int y \, dm \end{aligned}$$

First, in guild to detect $x_{CM}$, we shall slice the triangle into thin slices with mass $dm$, height y and thickness $dx$, as shown in the figure beneath. This is such that every indicate in $dm$ has the aforementioned x value (same distance from y-axis).

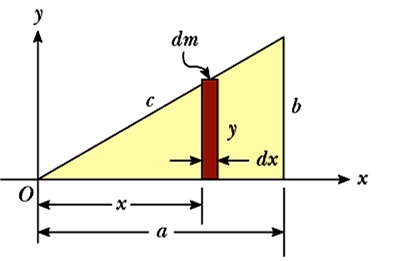
CM of right angle triangle

Wait at the figure higher up, from theory of similar triangles, we can obtain this relation:

$$\begin{aligned} \frac{y}{x} &= \frac{b}{a} \\ y &= \frac{b}{a} x \end{aligned}$$

Nosotros will use this relation in the calculation for $dm$ below.

The mass per unit area, $\rho$ is given past:

$$\begin{aligned} M &= \rho \left( \frac{1}{2} a b \correct) \\ &= \frac{2M}{ab} \end{aligned}$$

Hence, $dm$ will exist given by:

$$\begin{aligned} dm &= \rho \left( y \, dx \right) \\ &= \rho \left( \frac{b}{a} x \right) \, dx \terminate{aligned}$$

Using $dm$ in the equation for centre of mass:

$$\begin{aligned} x_{CM} &= \frac{one}{Thousand} \int x \, dm \\ &= \frac{\rho}{M} \int\limits_{0}^{a} x \left( \frac{b}{a} x \right) \, dx \\ &= \frac{one}{Thou} \frac{2M}{ab} \left[ \frac{b}{a} \frac{10^{three}}{iii} \right]_{0}^{a} \\ &= \frac{2}{ab} \left( \frac{b}{a} \frac{a^{3}}{3} \correct) \\ &= \frac{2}{3} a \end{aligned}$$

Now, to find $y_{CM}$, nosotros will choose $dm$ such that every bespeak in $dm$ has the same y value.

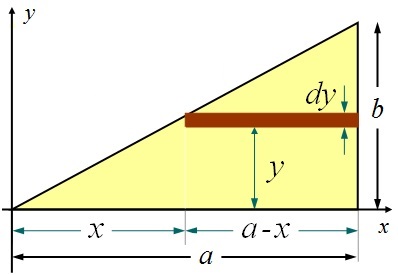
y CoM of right angle triangle

From the to a higher place effigy, using the theory of similar triangles, we can go far at a relation:

$$\begin{aligned} \frac{y}{10} &= \frac{b}{a} \\ x &= \frac{a}{b} y \end{aligned}$$

Hence, $dm$ is given by:

$$\begin{aligned} dm &= \rho \left( a-10 \right) dy \\ &= \rho \left( a-\frac{a}{b} y \correct) dy \cease{aligned}$$

Using $dm$ in the equation for centre of mass:

$$\begin{aligned} y_{CM} &= \frac{1}{M} \int y \, dm \\ &= \frac{\rho}{M} \int\limits_{0}^{b} y \left( a-\frac{a}{b} y \right) \, dy \\ &= \frac{1}{Yard} \frac{2M}{ab} \left[ \frac{ay^{two}}{2}-\frac{ay^{iii}}{3b} \right]_{0}^{b} \\ &= \frac{2}{ab} \left( \frac{ab^{two}}{2}-\frac{ab^{3}}{3b} \correct) \\ &= \frac{one}{three} b \terminate{aligned}$$

Side by side: Eye Of Mass Of A Cone

Previous: What is centre of mass?

Back To Mechanics (UY1)